
 [罗戈导读]选址问题是运筹学中非常经典的问题。该问题是指在确定选址对象,选址目标区,成本函数以及约束条件的前提下,以总物流成本最低或总服务水平最优或社会效益最大化为目标,确定物流系统中物流节点的数量,位置,从而合理规划物流网络结构。
[罗戈导读]选址问题是运筹学中非常经典的问题。该问题是指在确定选址对象,选址目标区,成本函数以及约束条件的前提下,以总物流成本最低或总服务水平最优或社会效益最大化为目标,确定物流系统中物流节点的数量,位置,从而合理规划物流网络结构。

陈立婷,北京航空航天大学电子信息工程学院在读研究生,研究方向:运筹优化算法设计与应用、枢纽选址、空中交通管理
顾少英,多伦多大学工业工程与运筹学研究生,研究方向: 应用统计,随机过程与优化,机器学习
江镕行,同济大学经济与管理学院硕博连读生,研究方向:优化算法设计及应用、物流与供应链、共享汽车
编者按
选址问题是运筹学中非常经典的问题。该问题是指在确定选址对象,选址目标区,成本函数以及约束条件的前提下,以总物流成本最低或总服务水平最优或社会效益最大化为目标,确定物流系统中物流节点的数量,位置,从而合理规划物流网络结构。
选址问题在公司实现其经营战略与目标的过程中有着重大的意义。选址的好坏直接影响到生产成本,服务时间,服务质量等等,进而影响公司的利润与其在商业市场上的竞争力,甚至决定了企业的命运。一个好的选址可以减少生产成本,节省顾客购买时间,便利顾客,而差的选址会带来物流中的不便与损失。由于选址是一项长期性投资,一旦确定下来就不能随意更改,因此规划其位置前必须进行深入的调查和周密的考虑。
选址问题,旨在选址目标区内确定设施的位置以及数量,并满足一定的约束条件,使得目标最优。选址问题根据规划区域,距离,目标有多种分类。
(1)规划区域
连续选址问题:设施可以在全平面内任意范围内选址。当选址区域过大,需考虑地球的球面效应时,规划区域为曲面。
离散选址问题:设施的候选位置为有限个。
(2)距离

欧几里得距离:两点间的直线距离;
方格线距离:两个点上在标准坐标系上的绝对轴距之总和。
图中绿色线段为两点间的欧几里得距离,黄色线,蓝色线,红色线为方格线距离。方格线距离也称为计程车几何或城市区块距离。
大圆距离:指的是从球面上两点间的最短距离。
(3)目标
单目标选址:总运输成本最低,总费用最低(包含运输成本,配送中心固定费用等),中枢纽数目最少,总服务最优。其中最低成本的目标函数为MiniSum形式,总服务最优的多为MiniMax形式。如应急设施选址时目标为使需求点尽可能快的得到应急服务。
多目标选址:单目标选址中的多个组合,可通过将多个单目标加权转化为单目标进行求解。
近年来,选址问题在物流管理,交通运输,通信电讯,医疗服务等领域有了广泛的研究和应用。下面介绍下几种常用的模型。
2.1 重心法选址模型
重心法适用于选址区域为连续平面,以欧几里得距离作为距离形式,以总运输成本最低为目标函数的选址问题。重心法选址模型来源于解析几何,其将物流网络中的需求点看作一平面内的点,把需求量作为重量,一般选取出这一平面内的需求点的重心点作为枢纽,以达到减少运输成本的目的。
重心法目标函数为:

2.2 p-中值(p-median)模型
p-中值问题中,选址区域为有限点组成的集合,距离形式为任意形式,目标函数为总运输成本最低。P-中值问题限制了枢纽个数为p个,每个需求点只能与一个枢纽建立连接,可用以下模型表示:

式中,(1)保证了每个需求点仅与一个枢纽节点有连接,(2)保证了备选节点集中只有被选中设为枢纽的节点可与需求点建立连接,(3)保证了枢纽个数为p个。
2.3 p-中心(p-center)模型
p-中心问题与p-中值问题的唯一不同点在于目标函数的形式。在p-中心问题中,目标函数为MinMax形式,目标是使每个需求点到最近设施的最大距离最小,通常用于消防站,警察局等应急设施的选址中。如消防站设施选址问题中,目标为使区域内的每个用户都能在某个阈值时间内得到消防服务,在满足约束的条件下,该阈值越小越好。
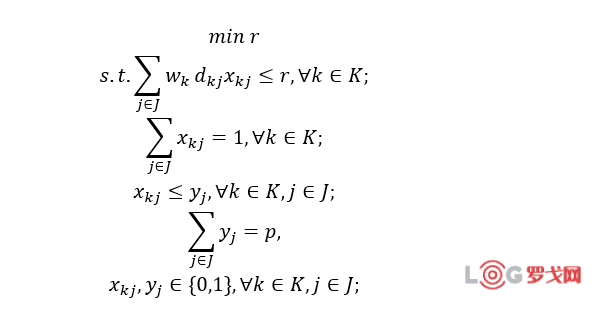
2.4 集合覆盖模型
集合覆盖模型是指在覆盖所有需求点的前提下,使得总建设费用最低,当每个设施的建设费用相同时,问题简化为枢纽数目最少,该模型可以表示为:

下面我们辅以一个简单的例子来详细介绍重心法的求解过程:
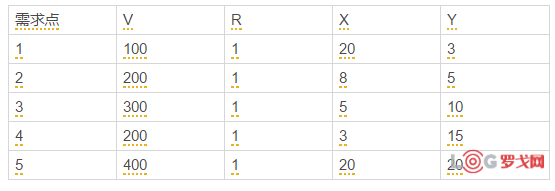
如图所示,共有五个需求点,其各自对应的V,R,X,Y如表所示,
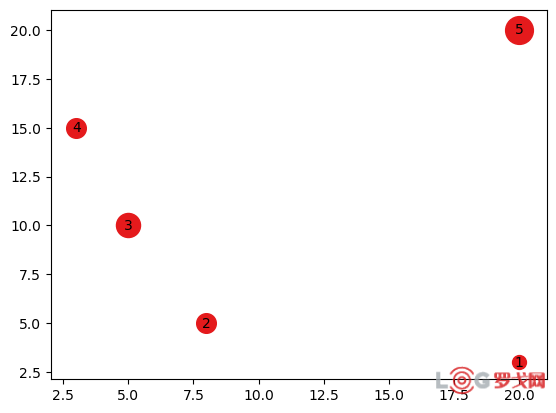
3.1 单设施选址问题:
单设施选址问题的一般求解使用的是迭代重心法,注意到目标函数的形式为:
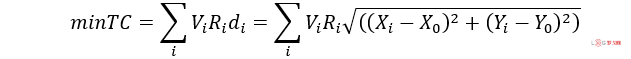
求偏导数可得:
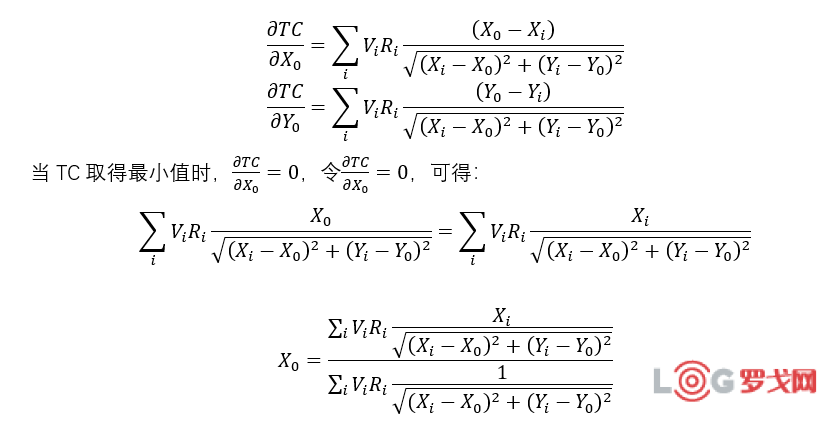

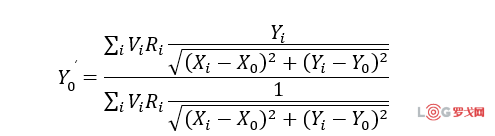
则迭代法的整个流程为:
1) 使用等效重心公式,求得初始等效重心作为初始解,计算花费cost1
2) 使用迭代重心公式,求得迭代后的解,计算花费cost2
3) 比较cost1和cost2,如相等或相差小于阈值,迭代结束,此时的解即为最终的解;否则令cost1=cost2,回到步骤2)
结合例子来看,使用各个需求点的等效重心坐标作为初始解,
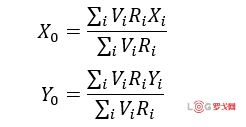
在此例子中等效重心坐标为 (12.4167,12.75)(图中黑点所示),此时总费用为11323.90
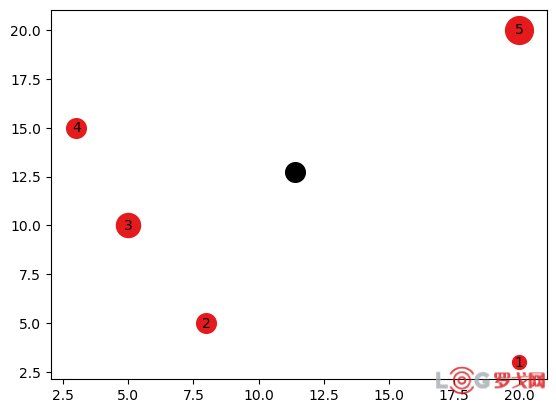
要注意,初始解大部分情况下不是最优解。
举一个简单的例子,如在(0,0)处需求点P 需求量为10,(10,0)点处需求点Q需求量为1,根据直接重心法仓库应选址在(1,0)处,此时花费为19。然而若直接选址在(0, 0)处,总花费仅为10。
当二十次迭代时,
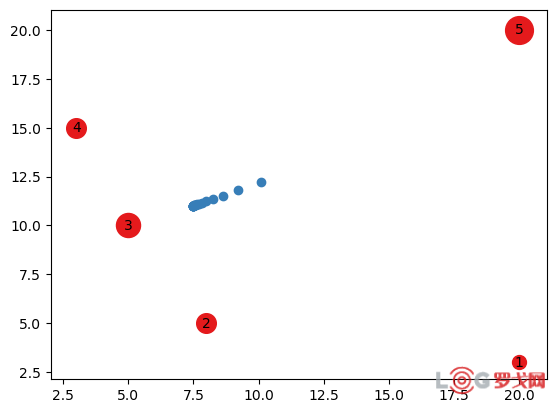
可以看到,解趋于稳定,最终的花费为10861.30。
3.2 多设施选址问题
多设施选址问题较单设施选址问题复杂得多,一种常用解法是将其看成多个单设施选址问题来解决。对于一个p设施选址问题来说,求解步骤如下:
1) 随机选择p个初始坐标作为初始解,计算花费cost1
2) 使用当前解,将每个需求点分配个距离最近的设施,从而得到p个需求点簇,在每个需求点簇内迭代得解,计算花费cost2
3) 比较cost1和cost2,如相等或相差小于阈值,迭代结束,此时的解即为最终的解;否则令cost1=cost2,令迭代后的解作为当前解,回到步骤2)
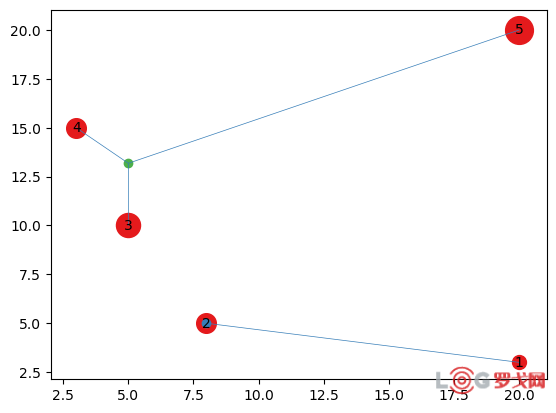
以p=2为例,
初始解花费为10534:
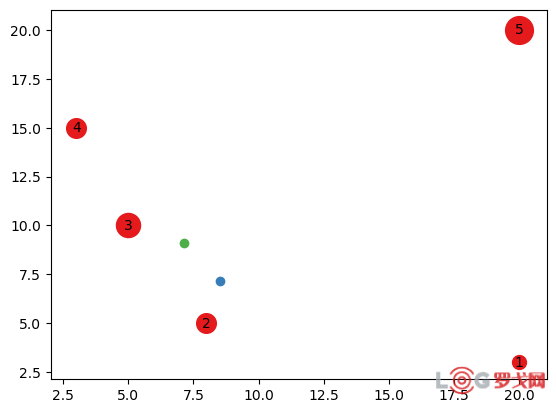
迭代二十次后,解已经稳定,此时最终解为9302.43:
3.3其他求解方法
上文介绍了重心法求解单设施选址问题和多设施选址问题,但重心法的应用场景有限,仅适应于约束简单的选址问题,当问题变得复杂,约束条件增加或目标函数改变时就难以适用,本节简单介绍了一些方法求解更复杂的选址问题。
1.解析解
求解纯数学模型,获得最优解。然而本文提到的几个选址问题均为NP-Hard问题,在问题规模较小时可通过CPLEX、Gurobi等求解器求解,但随着问题规模扩大,在多项式时间内无法获得解析解。
2.近似解
该方法是解析解的改编方法,常见的方式为采用松弛算法将约束吸收到目标函数中,减少求解的复杂程度,减少求解时间,但同样无法应对大规模问题。
3.启发式算法
该方法是较为常用的求解NP-Hard问题的方法,如遗传算法、蚁群算法、粒子群算法等,思路是随机产生多个初始解,通过特殊的迭代寻优规则进行优化并更新状态,到达一定迭代次数或者其他终止条件时结束。此类算法在应对大规模问题时往往求解时间短,一般均能得到一个较优的可行解,确点是容易陷入局部最优,无法得到最优解,同时求解过程与问题高度相关,改变问题结构对算法影响很大,难以扩展。
4.仿真法
对于大型、复杂的选址问题,可通过仿真的方式重现系统活动。一般而言,采用仿真时需要对现实情况有较好的统计,获取一些关键参数的统计分布,对实践的要求较高。与其他方法相比,仿真方法对计算机的算力要求较小,不需要严格的编程。
4.1.仓储资源规划与布局项目
由于业务扩张需求,某公司希望在湖南省内进一步优化当前的供应链仓网布局: 其中几个重要板块包括如何在考虑现有销售信息和仓储布局下,增添新的前置仓库以满足业务的增长需求;如何根据历史订单数据/仓储成本/运输价格,寻找供应链成本最低模型与最优库存策略;如何基于当前仓网布局与其他可获得信息周期性地预测库存与峰值,并可视化,等等。在该项目中,悠桦林基于大规混合整数规划模型,开发客户可视化前端,力图建立全面的仓网规划能力,为仓储网络决策的科学性和精准性提供系统支持。
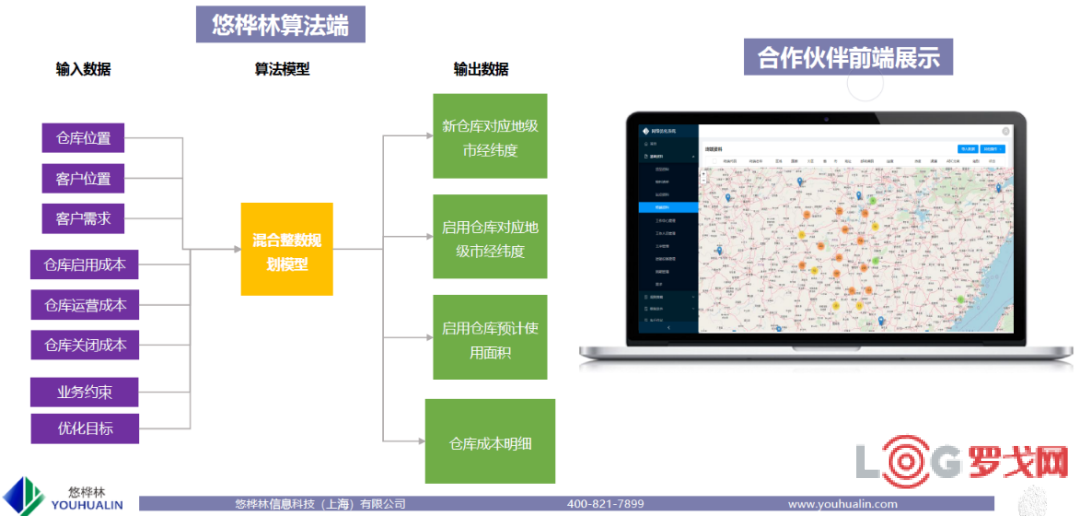
4.2.项目背景回顾
本文着重介绍其中的前置仓库选址问题: 即如何在诸多条件约束下(具体参见下一节),选择数量最少的新前置仓库地址,以满足对整个湖南省的门店的服务支持。同时输出每个门店的具体地理位置。

4.3. 前置仓选址方案
该混合整数规划的建模思想为2.4节的集合覆盖模型的加强衍生升级版。这里主要想介绍的是这个项目所特有的若干约束项/前提条件,包括但不限制于
· 前置仓所选地址的最大范围边界(湖南省)
· 每个前置仓服务半径为150KM的圆
· 一个门店仅能被一个前置仓服务且总覆盖率至少达到95%
· 每个门店所需总量额的范围上下限
同时设定成本系数,包括但不限制于
· 仓库存储成本
· 仓库与门店间的运输成本
优化目标
· 最小化仓库数量
输出结果
· 仓库数量与每个仓库对应的地理位置
此外,悠桦林额外在这里为该公司提供了两种可选约束条件下的优化策略与结果:
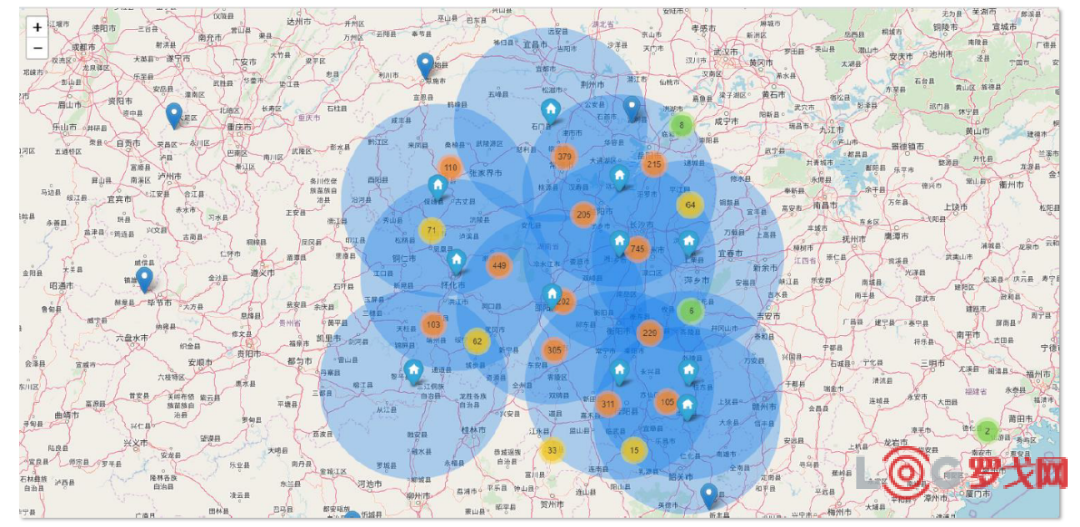
· 所有客户一视同仁,至少满足95%客户服务水平,此时优化结果为11仓
· 更好的服务大客户,至少满足95%需求覆盖率,此时优化结果为8仓
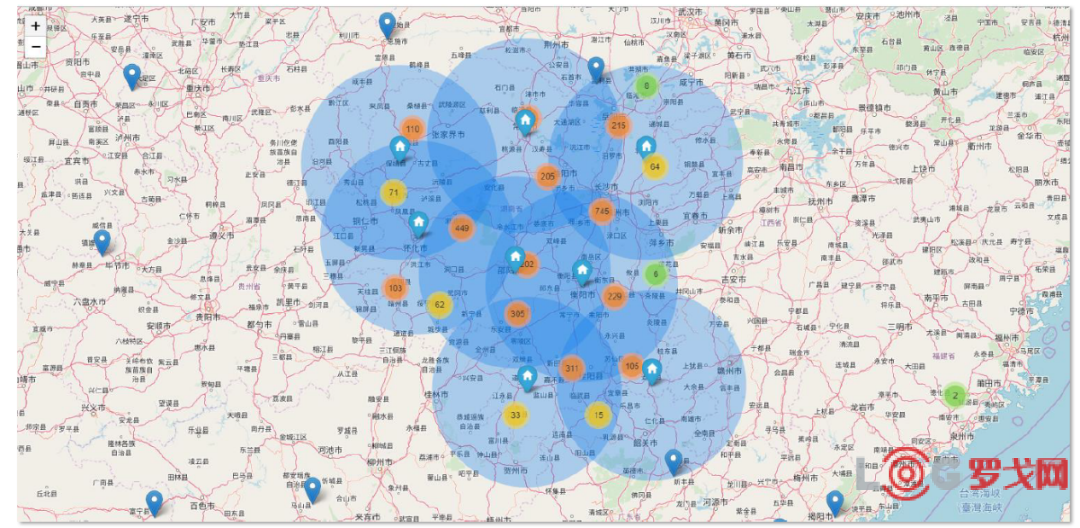
最终,对比两种优化结果,第二种可选约束条件下总仓数更少且总距离最短,以下为两种结果对比:

在该项目中,悠桦林基于大规模混合整数规划模型,为该公司提供了最优化的前置仓库选址方案,同时为客户提供了多种可选约束条件,与相应的不同种决策方案。以上仓库选择问题为悠桦林为该公司指定的供应链网络全局规划的一个重要环节,为全网布局预测与优化提供输入。
参考文献:
Facility Location and Strategic Supply Chain Management, Prof. Dr. Stefan Nickel, 2008-2009